
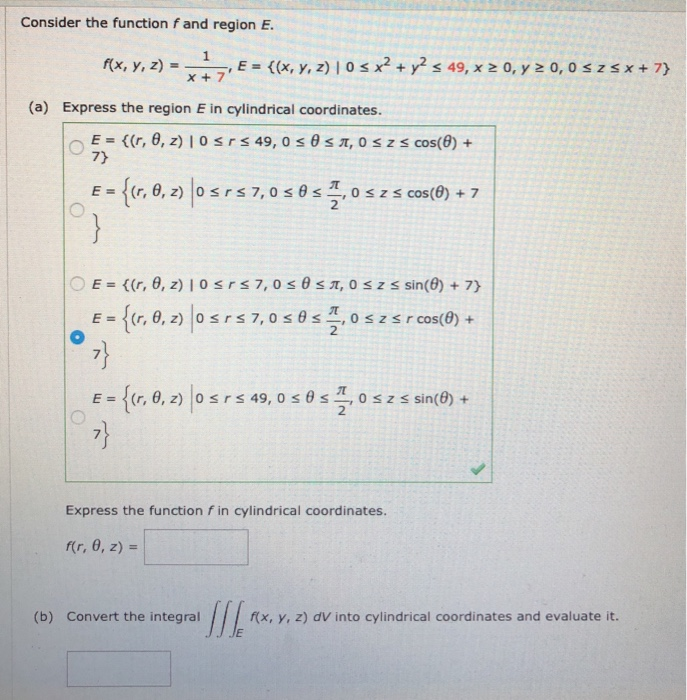
Solved Let F X Y X 2 Y 2 E Y 2 X 2 Find F X And Chegg Com
Tangent plane to (x^2 2 y^2) 1 at (x,y)=(1,2) nearest Supercut;Simplifying y = f(x 2) Reorder the terms y = f(2 x) y = (2 * f x * f) y = (2f fx) Solving y = 2f fx Solving for variable 'y' Move all terms containing y to the left, all other terms to the right Simplifying y = 2f fx You can always share this solution See similar equations
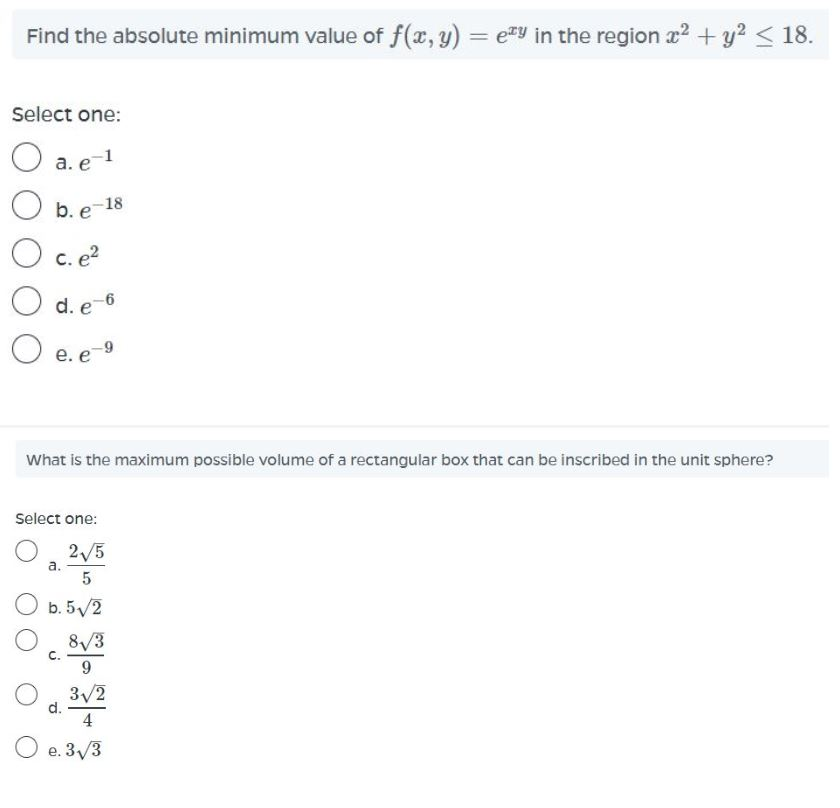
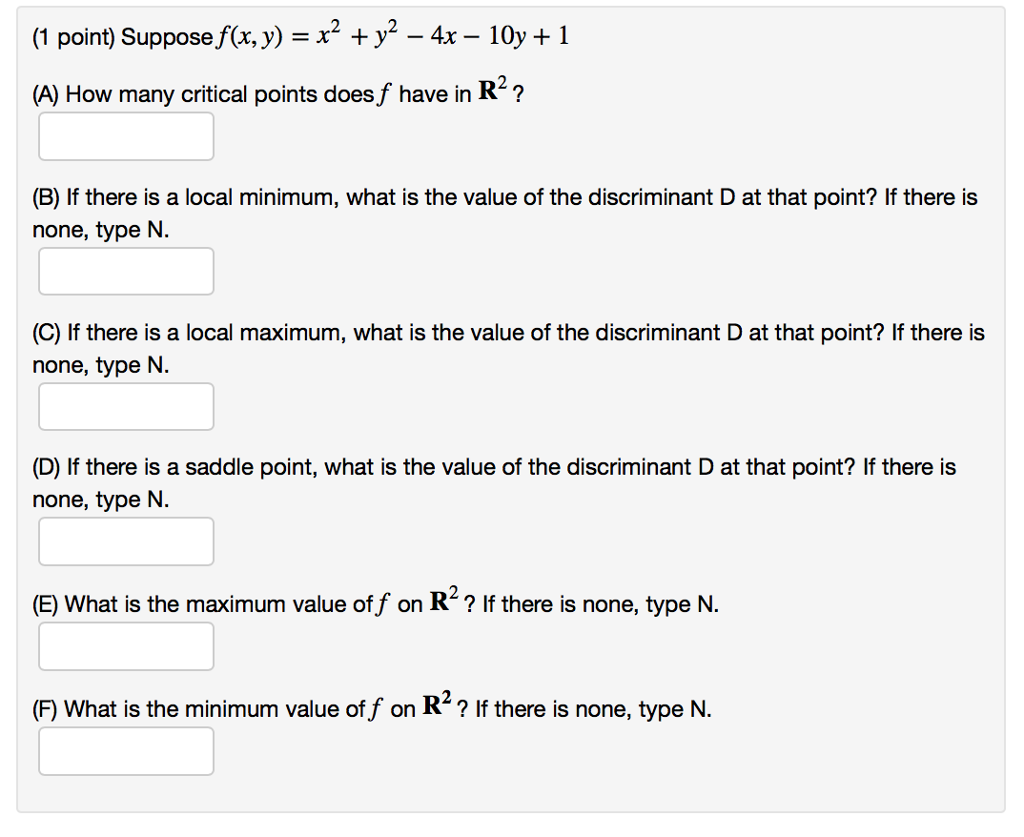
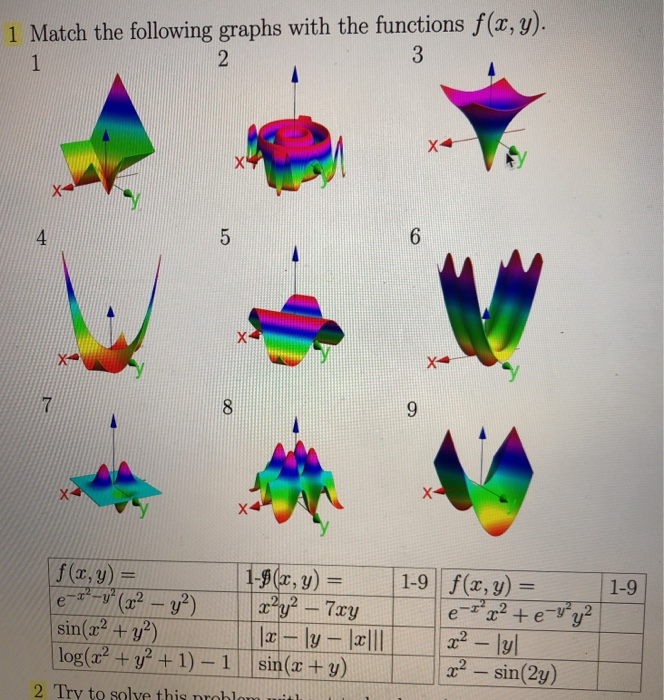
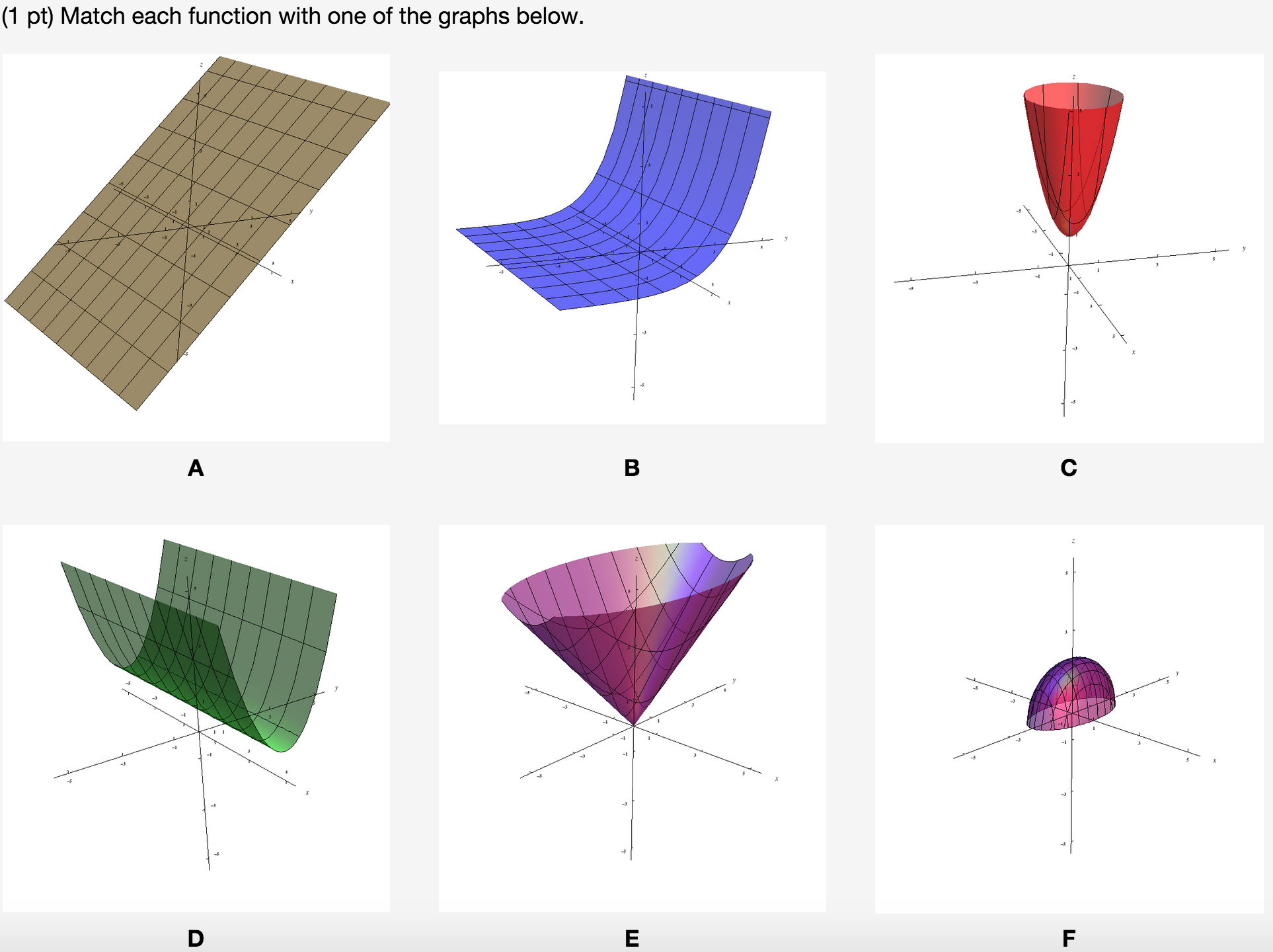
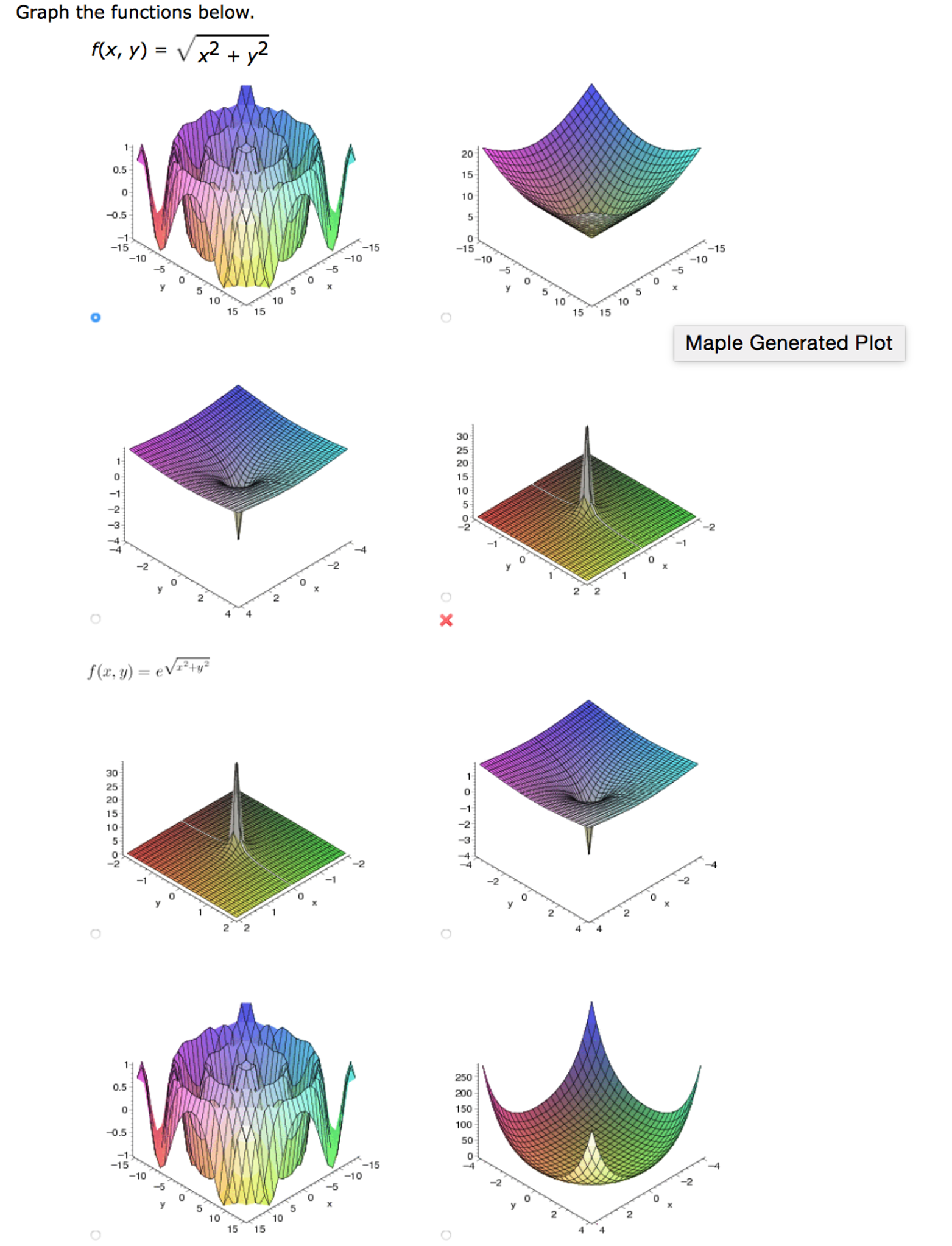
Domain of f(x y)=e^-(x^2+y^2)
Domain of f(x y)=e^-(x^2+y^2)-Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Replace the variable x x with − 1 1 in the expression f ( − 1) = ( − 1) 2 − 2 f ( 1) = ( 1) 2 2 Simplify the result This problem has been solved!

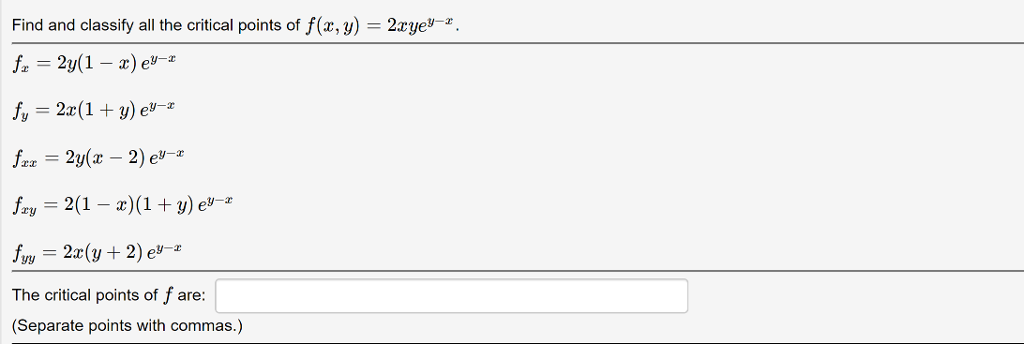
Solved We Have The Following F X Y Z 4 X2 Y2 Z 2 X2 Chegg Com
$\begingroup$ @David By "res no longer existed," you perhaps meant that your kernel crashed At least mine did But it seems to work if you take it in stages dom = res3;The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction y^ {2}2xyx^ {2}=0 y 2 2 x y x 2 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2x for b, and x^ {2} for c in the quadratic formula,Calculadora gratuita de funciones encontrar el dominio y rango de una función, puntos de intersección, extremos de una función y asíntotas paso por paso
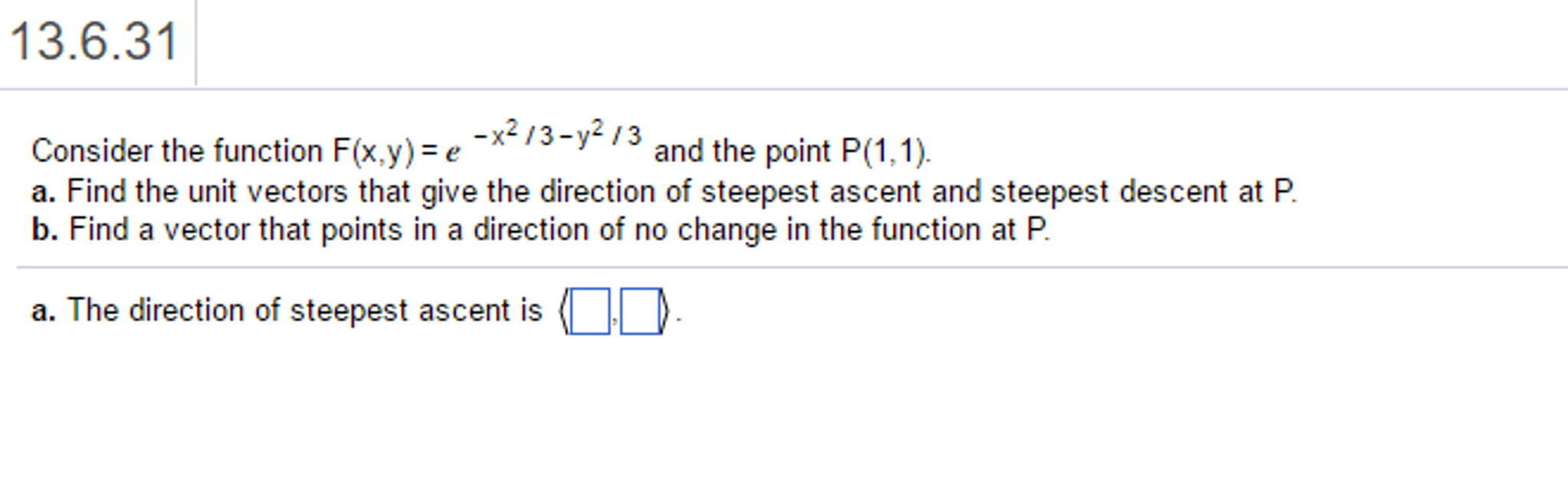
We have f(x,y) = xy e^(x^2y^2) Step 1 Find the Partial Derivatives We compute the partial derivative of a function of two or more variables by differentiating wrt one variable, whilst the other variables are treated as constantProof As we know, X and Y are independent if and only if fX;Y(x;y) = fX(x)fY(y) or, equivalently, fXjY(xjy)= fX(x) But then E(XjY =y)=åx xfXjY(xjy)=åx xfX(x)=E(X) 2 2 EE(g(X)jY)=E(g(X)) Proof Set Z = g(X) Statement (i) of Theorem 1 applies to any two rv's Hence, applying it to Z and Y we obtain EE(ZjY)= E(Z) which is the same as EE(g(X)jY)= E(g(X)) 2 In a marketing context, the outcome (Y) could equal the number of product sales, where the function (f) could be an email opened from a newsletter campaign, and the input (x) could be the number of coupons within the email As you increase the number of coupons (x), then the function of email opens (f) yields more product sales (Y)
Domain of f(x y)=e^-(x^2+y^2)のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「Domain of f(x y)=e^-(x^2+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
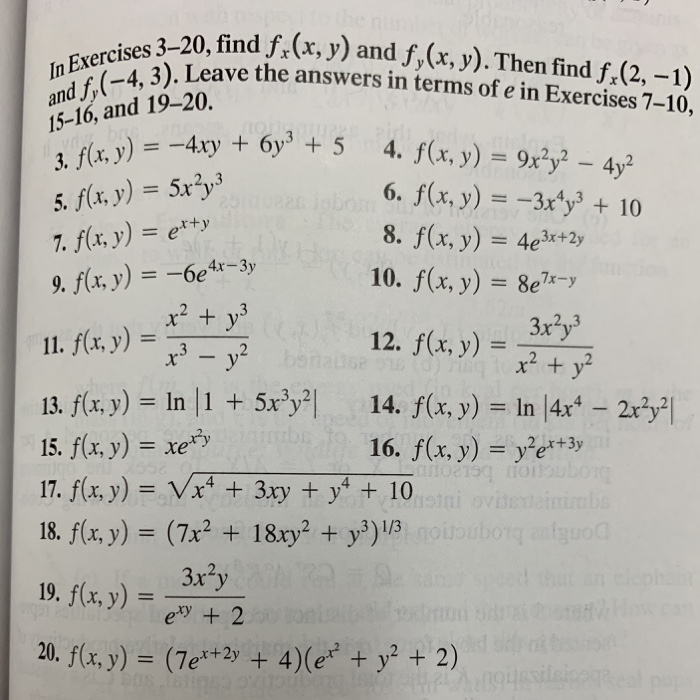 |  |  |
「Domain of f(x y)=e^-(x^2+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | 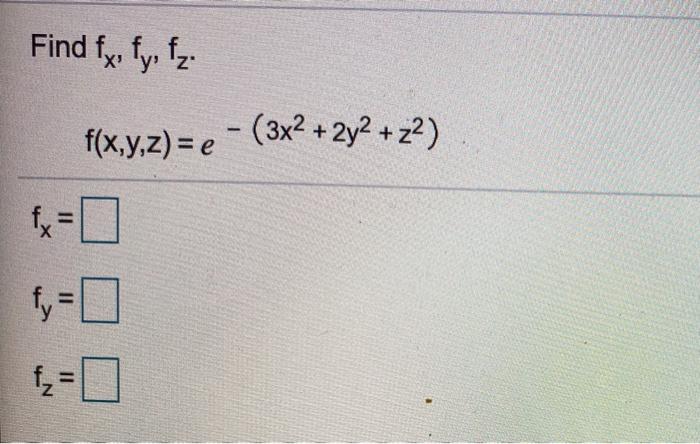 |
「Domain of f(x y)=e^-(x^2+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 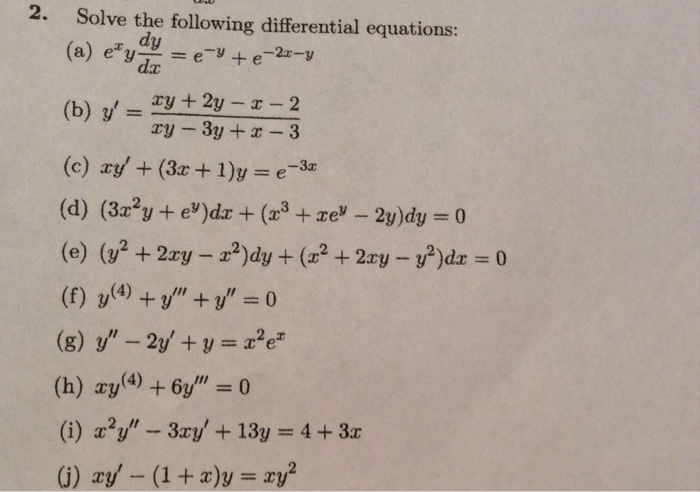 | |
「Domain of f(x y)=e^-(x^2+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Domain of f(x y)=e^-(x^2+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
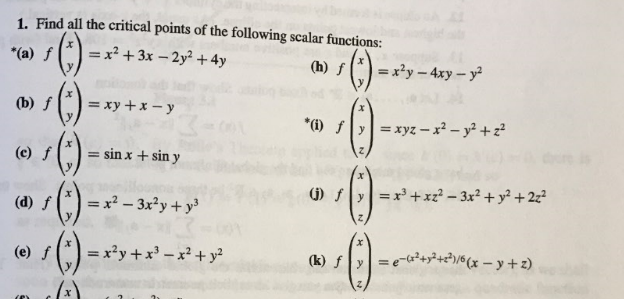 |  |  |
「Domain of f(x y)=e^-(x^2+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
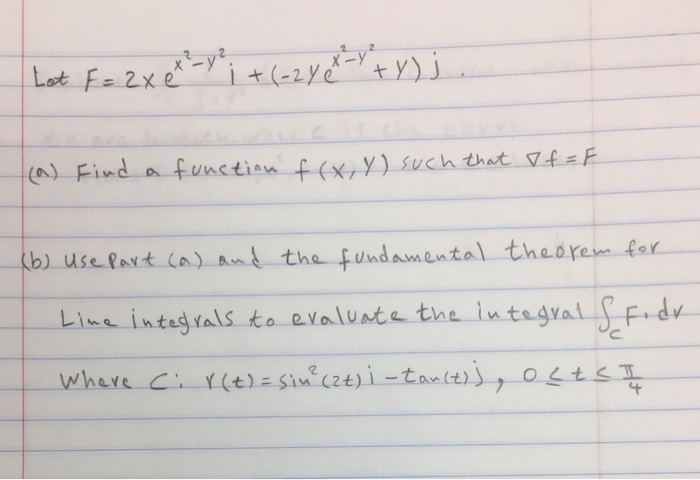 |  |  |
「Domain of f(x y)=e^-(x^2+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 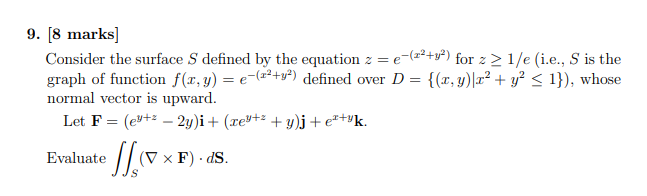 | |
 |  |  |
「Domain of f(x y)=e^-(x^2+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「Domain of f(x y)=e^-(x^2+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
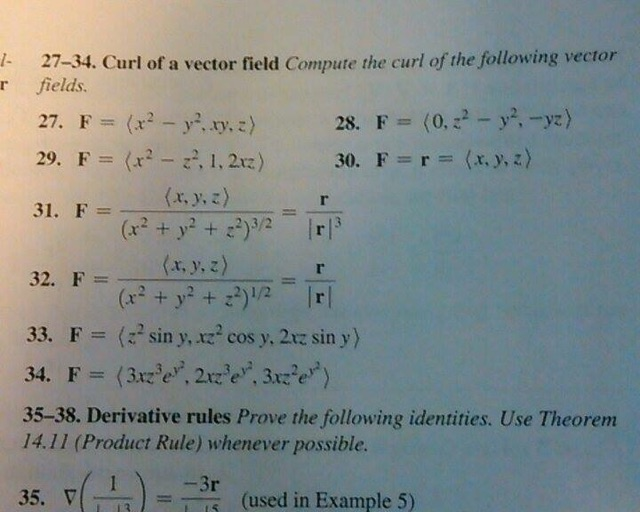 |  |  |
 |  | |
 |  |  |
「Domain of f(x y)=e^-(x^2+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Domain of f(x y)=e^-(x^2+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
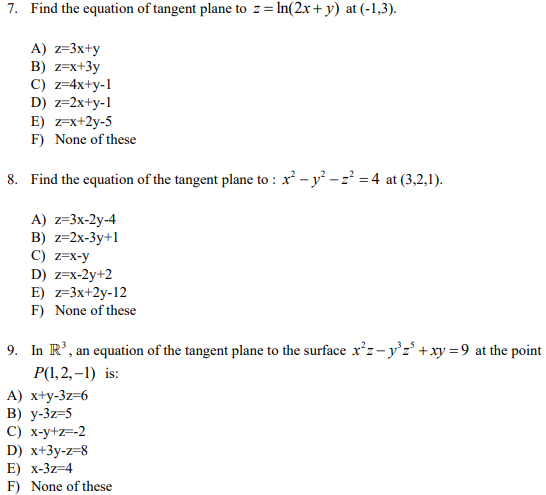 |  |
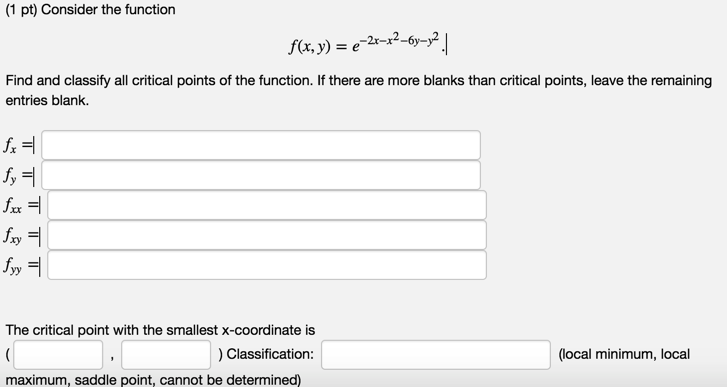
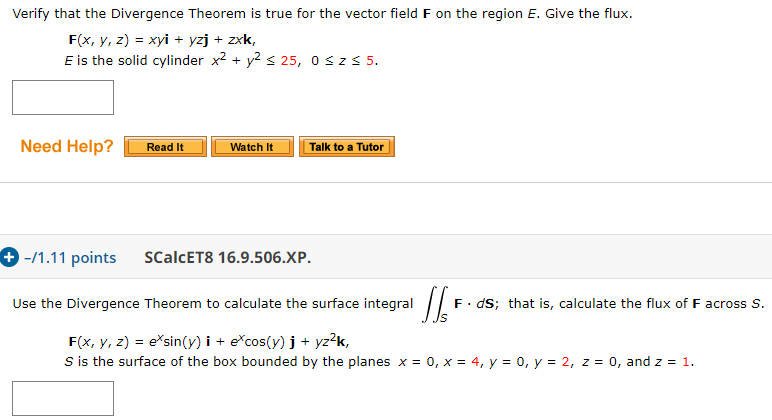
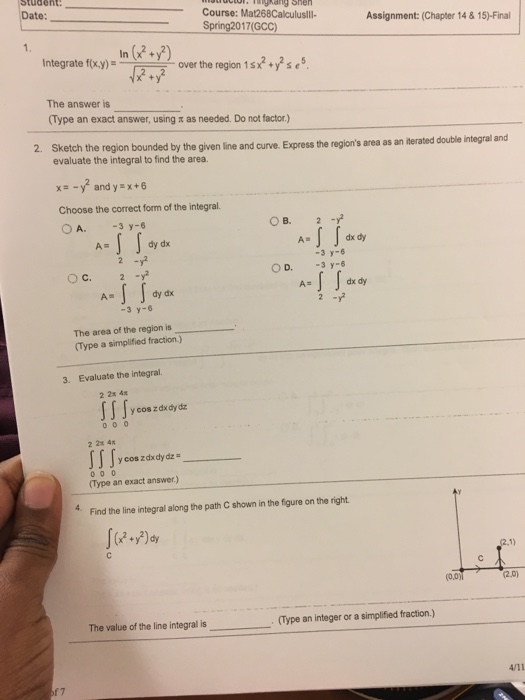
It suffices to show that f ′ ( x) = 0 for all x ∈ R We see that the given condition implies f ( x) − f ( y) x − y ≤ x − y So in a δ neighborhood of x, the quotient in definition of the derivative is less than δ So the limit is 0, and we are done Share Follow this answer to receive notificationsSee the answer See the answer See the answer done loading f (x,y)= (x^2y^2) e^x Expert Answer Who are the experts?
Incoming Term: f(x y)=e^-(x^2+y^2), f(x y)=4-x^2-y^2, f(x y)=3-x^2-y^2 graph, f(x y)=e^(4y-x^2-y^2), f(x y)=sqrt(4-x^2-y^2), domain of f(x y)=e^-(x^2+y^2), f(x y)=sqrt(4-4x^2-y^2), f(x y)=x^4-2x^2+y^3-3y, f(x y)=(x^3y-xy^3)/(x^2+y^2), f(x y)=x^2+y^4+2xy,




0 件のコメント:
コメントを投稿